Vamos a trabajar las intersecciones en los siguientes casos:
1. Intersección de RECTAS r y s.
2. Intersección de PLANOS (alpha y beta)
3. Intersección RECTA-PLANO. (En la siguiente entrada).
1. Intersección de RECTAS r y s.
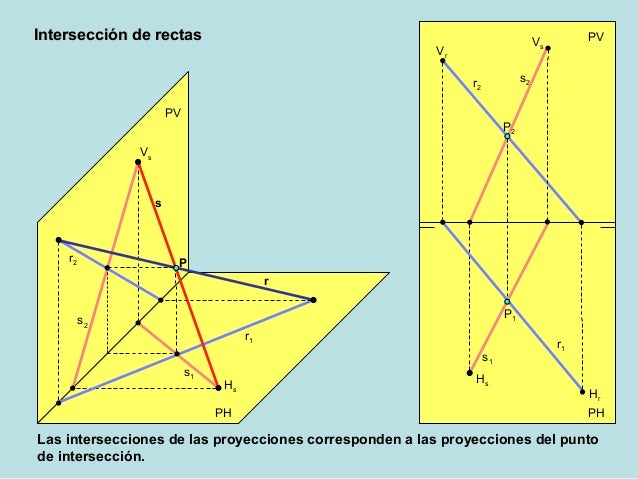
La intersección de dos rectas r y s es...un punto P.
Como el punto P pertenece a ambas rectas, debe cumplir... el PRIMER CRITERIO de pertenencia:
(Un punto pertenece a una recta cuando las PROYECCIONES del punto pertenecen a las PROYECCIONES de la recta).
r2 y s2 se cortan en P2
r1 y s1 se cortan en P1
RECTAS SECANTES.
Para que dos rectas SE CORTEN, deben tener un punto en común.
En este caso ese punto es un PUNTO PROPIO P.
r2 y s2 se cortan en P2
r1 y s1 se cortan en P1
P2 y P1 están alineadas según una recta perpendicular a LT.
(Dos rectas secantes son COPLANARIAS. Determinan un plano y sólo uno).
 RECTAS PARALELAS.
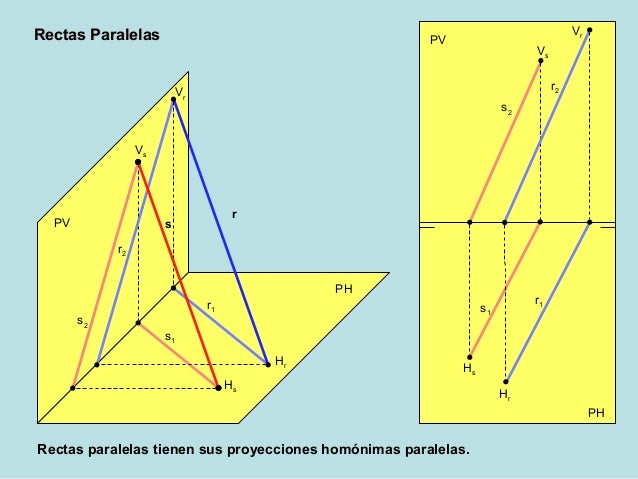
RECTAS PARALELAS.
Para que dos rectas sean PARALELAS, deben tener CORTARSE EN EL INFINITO.
En este caso ese punto es un PUNTO IMPROPIO P 8
r2 y s2 se cortan en P2 8
r1 y s1 se cortan en P1 8
(Dos rectas paralelas son COPLANARIAS. Determinan un plano y sólo uno).
 RECTAS QUE SE CRUZAN.
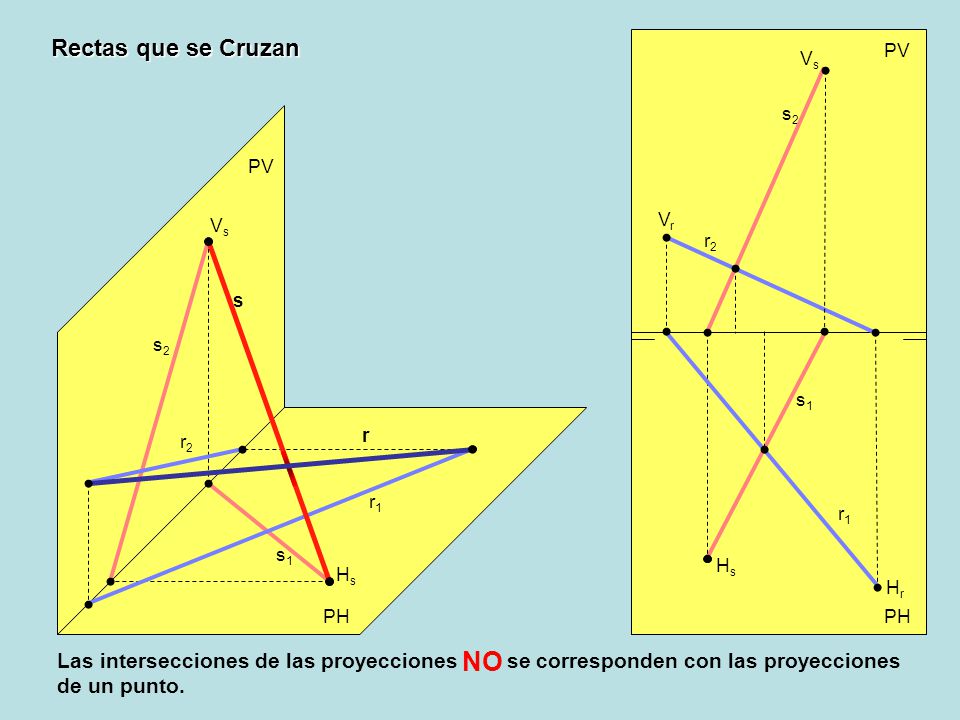
RECTAS QUE SE CRUZAN.
No existe intersección. No tienen puntos en común.
r2 y s2 se cortan en P2 8
r1 y s1 se cortan en P1 8
P2 y P1 NO están alineadas según una recta perpendicular a LT.
(Dos rectas que se cruzan NO son COPLANARIAS. No pueden pertenecer a un mismo plano).
 2. Intersección de PLANOS (alpha y beta)
2. Intersección de PLANOS (alpha y beta)
La intersección de dos planos
alpha y
beta es...una
recta r
Como la recta r pertenece a ambos planos, debe cumplir... el segundo criterio de pertenencia:
(Una recta pertenece a un plano cuando las TRAZAS de la recta pertenecen a las TRAZAS del plano)
alpha2 y beta2 se cortan en la traza de la recta Vr
alpha2 y beta2 se cortan en la traza de la recta Vr
NOTA DE NOMENCLATURA:
En esta imagen y en las láminas que vais a descargar,
se usa otra nomenclatura.
Si queréis la cambiáis a la que utilizamos en clase.
Las trazas del plano serían:
Alpha2=P´ Alpha1=P Beta2=Q´ Beta1=Q
Las proyecciones de la recta i serían:
Las trazas de la recta i serían:
LÁMINAS 1, 2, 3 y 4, Descarga estas láminas de intersecciones para trabajar.
(Como ves hay láminas que trabajaremos más adelante. De momento haced la 1 ,la 2 ) La 3 se resuelve con la teoría de la entrada siguiente 3.3).
SOLUCIONES Aquí tienes las soluciones a todas esa láminas.


















